weird 3d shapes to draw
d3-shape
Visualizations typically consist of detached graphical marks, such as symbols, arcs, lines and areas. While the rectangles of a bar chart may be easy enough to generate directly using SVG or Canvass, other shapes are complex, such as rounded annular sectors and centripetal Catmull–Rom splines. This module provides a variety of shape generators for your convenience.
As with other aspects of D3, these shapes are driven past information: each shape generator exposes accessors that control how the input data are mapped to a visual representation. For example, you might define a line generator for a time series past scaling fields of your information to fit the nautical chart:
const line = d3 . line ( ) . 10 ( d => x ( d . date ) ) . y ( d => y ( d . value ) ) ; This line generator can then exist used to compute the d aspect of an SVG path element:
path . datum ( data ) . attr ( "d" , line ) ; Or you tin use information technology to render to a Canvas 2D context:
line . context ( context ) ( information ) ; For more, read Introducing d3-shape.
Installing
If you use npm, npm install d3-shape. Yous can also download the latest release on GitHub. For vanilla HTML in modern browsers, import d3-shape from Skypack:
< script type="module"> import { line } from "https://cdn.skypack.dev/d3-shape@3" ; const l = line ( ) ; </ script >
For legacy environments, you can load d3-shape'south UMD bundle from an npm-based CDN such as jsDelivr; a d3 global is exported:
< script src="https://cdn.jsdelivr.internet/npm/d3-path@3"> </ script > < script src="https://cdn.jsdelivr.internet/npm/d3-shape@3"> </ script > < script > const l = d3 . line ( ) ; </ script > API Reference
- Arcs
- Pies
- Lines
- Areas
- Curves
- Custom Curves
- Links
- Symbols
- Custom Symbol Types
- Stacks
Note: all the methods that have arrays also have iterables and convert them to arrays internally.
Arcs
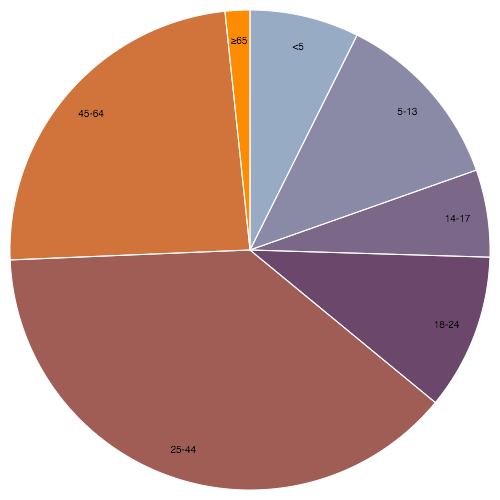
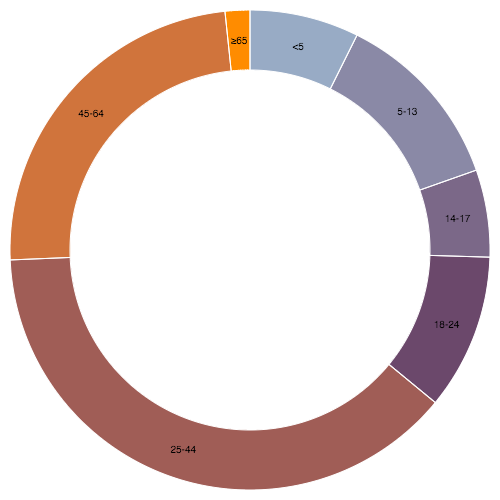
The arc generator produces a circular or annular sector, every bit in a pie or donut nautical chart. If the absolute divergence betwixt the outset and end angles (the angular span) is greater than τ, the arc generator will produce a consummate circle or annulus. If it is less than τ, the arc's angular length volition be equal to the absolute deviation between the two angles (going clockwise if the signed difference is positive and anticlockwise if it is negative). If the absolute difference is less than τ, the arc may have rounded corners and angular padding. Arcs are always centered at ⟨0,0⟩; employ a transform (see: SVG, Canvass) to move the arc to a different position.
See also the pie generator, which computes the necessary angles to correspond an array of data as a pie or donut chart; these angles can then be passed to an arc generator.
# d3.arc() · Source
Constructs a new arc generator with the default settings.
# arc(arguments…) · Source
Generates an arc for the given arguments. The arguments are arbitrary; they are only propagated to the arc generator'south accessor functions along with the this object. For example, with the default settings, an object with radii and angles is expected:
const arc = d3 . arc ( ) ; arc ( { innerRadius: 0 , outerRadius: 100 , startAngle: 0 , endAngle: Math . PI / 2 } ) ; // "M0,-100A100,100,0,0,1,100,0L0,0Z" If the radii and angles are instead defined every bit constants, yous can generate an arc without whatever arguments:
const arc = d3 . arc ( ) . innerRadius ( 0 ) . outerRadius ( 100 ) . startAngle ( 0 ) . endAngle ( Math . PI / 2 ) ; arc ( ) ; // "M0,-100A100,100,0,0,1,100,0L0,0Z" If the arc generator has a context, then the arc is rendered to this context equally a sequence of path method calls and this function returns void. Otherwise, a path data string is returned.
# arc.centroid(arguments…) · Source
Computes the midpoint [x, y] of the middle line of the arc that would be generated by the given arguments. The arguments are arbitrary; they are simply propagated to the arc generator'due south accessor functions along with the this object. To be consistent with the generated arc, the accessors must be deterministic, i.e., return the same value given the same arguments. The midpoint is defined every bit (startAngle + endAngle) / 2 and (innerRadius + outerRadius) / 2. For example:
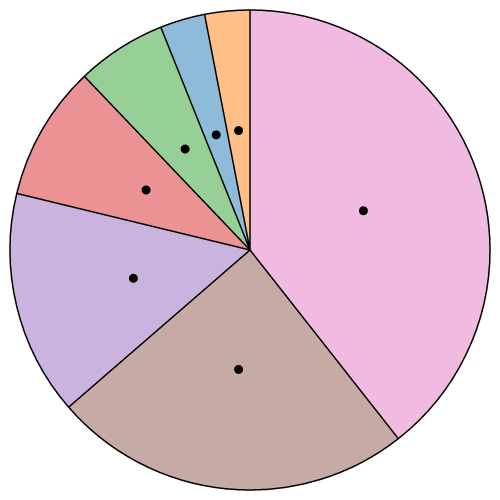
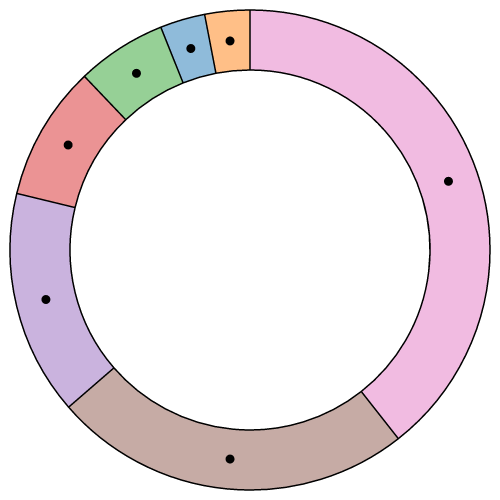
Annotation that this is not the geometric center of the arc, which may be exterior the arc; this method is merely a convenience for positioning labels.
# arc.innerRadius([radius]) · Source
If radius is specified, sets the inner radius to the specified office or number and returns this arc generator. If radius is not specified, returns the electric current inner radius accessor, which defaults to:
function innerRadius ( d ) { return d . innerRadius ; } Specifying the inner radius equally a function is useful for constructing a stacked polar bar nautical chart, ofttimes in conjunction with a sqrt scale. More commonly, a abiding inner radius is used for a donut or pie chart. If the outer radius is smaller than the inner radius, the inner and outer radii are swapped. A negative value is treated every bit nil.
# arc.outerRadius([radius]) · Source
If radius is specified, sets the outer radius to the specified part or number and returns this arc generator. If radius is not specified, returns the electric current outer radius accessor, which defaults to:
part outerRadius ( d ) { return d . outerRadius ; } Specifying the outer radius as a function is useful for constructing a coxcomb or polar bar chart, often in conjunction with a sqrt calibration. More than commonly, a constant outer radius is used for a pie or donut chart. If the outer radius is smaller than the inner radius, the inner and outer radii are swapped. A negative value is treated as cypher.
# arc.cornerRadius([radius]) · Source
If radius is specified, sets the corner radius to the specified function or number and returns this arc generator. If radius is not specified, returns the electric current corner radius accessor, which defaults to:
function cornerRadius ( ) { return 0 ; } If the corner radius is greater than zero, the corners of the arc are rounded using circles of the given radius. For a circular sector, the two outer corners are rounded; for an annular sector, all iv corners are rounded. The corner circles are shown in this diagram:
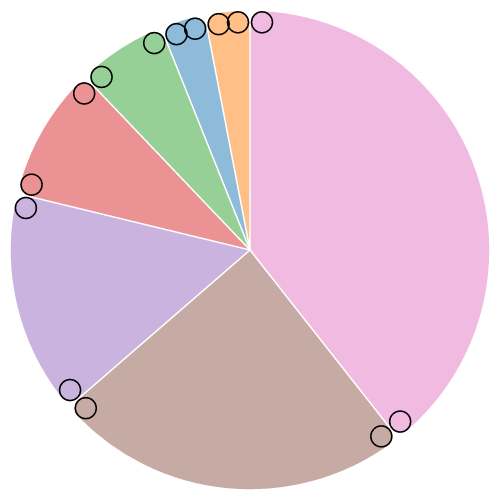
The corner radius may not exist larger than (outerRadius - innerRadius) / 2. In addition, for arcs whose athwart span is less than π, the corner radius may exist reduced equally 2 side by side rounded corners intersect. This is occurs more oftentimes with the inner corners. Run across the arc corners animation for analogy.
# arc.startAngle([angle]) · Source
If angle is specified, sets the commencement bending to the specified function or number and returns this arc generator. If angle is non specified, returns the current start bending accessor, which defaults to:
function startAngle ( d ) { return d . startAngle ; } The angle is specified in radians, with 0 at -y (12 o'clock) and positive angles proceeding clockwise. If |endAngle - startAngle| ≥ τ, a complete circle or annulus is generated rather than a sector.
# arc.endAngle([angle]) · Source
If bending is specified, sets the cease angle to the specified function or number and returns this arc generator. If angle is not specified, returns the electric current end bending accessor, which defaults to:
function endAngle ( d ) { return d . endAngle ; } The bending is specified in radians, with 0 at -y (12 o'clock) and positive angles proceeding clockwise. If |endAngle - startAngle| ≥ τ, a complete circumvolve or annulus is generated rather than a sector.
# arc.padAngle([angle]) · Source
If bending is specified, sets the pad angle to the specified role or number and returns this arc generator. If angle is non specified, returns the electric current pad bending accessor, which defaults to:
role padAngle ( ) { render d && d . padAngle ; } The pad angle is converted to a fixed linear altitude separating adjacent arcs, defined as padRadius * padAngle. This distance is subtracted equally from the start and stop of the arc. If the arc forms a consummate circle or annulus, as when |endAngle - startAngle| ≥ τ, the pad bending is ignored.
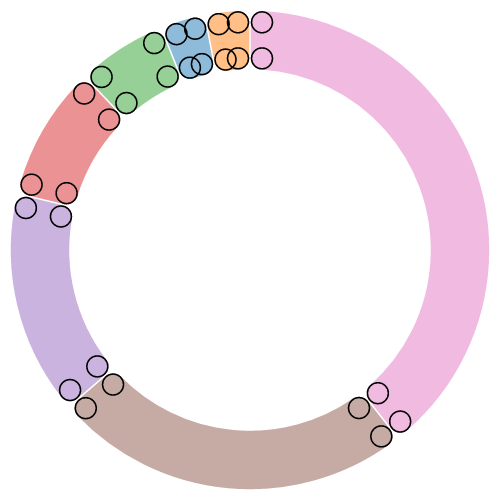
If the inner radius or angular span is pocket-size relative to the pad angle, it may not exist possible to maintain parallel edges betwixt adjacent arcs. In this case, the inner edge of the arc may plummet to a indicate, similar to a round sector. For this reason, padding is typically but applied to annular sectors (i.e., when innerRadius is positive), as shown in this diagram:
The recommended minimum inner radius when using padding is outerRadius * padAngle / sin(θ), where θ is the angular span of the smallest arc earlier padding. For case, if the outer radius is 200 pixels and the pad angle is 0.02 radians, a reasonable θ is 0.04 radians, and a reasonable inner radius is 100 pixels. See the arc padding animation for analogy.
Often, the pad bending is not set directly on the arc generator, but is instead computed by the pie generator so every bit to ensure that the area of padded arcs is proportional to their value; see pie.padAngle. See the pie padding animation for analogy. If you apply a abiding pad angle to the arc generator directly, it tends to subtract disproportionately from smaller arcs, introducing distortion.
# arc.padRadius([radius]) · Source
If radius is specified, sets the pad radius to the specified office or number and returns this arc generator. If radius is not specified, returns the current pad radius accessor, which defaults to goose egg, indicating that the pad radius should be automatically computed as sqrt(innerRadius * innerRadius + outerRadius * outerRadius). The pad radius determines the fixed linear distance separating adjacent arcs, divers as padRadius * padAngle.
# arc.context([context]) · Source
If context is specified, sets the context and returns this arc generator. If context is non specified, returns the current context, which defaults to null. If the context is not null, then the generated arc is rendered to this context as a sequence of path method calls. Otherwise, a path information string representing the generated arc is returned.
Pies
The pie generator does non produce a shape directly, but instead computes the necessary angles to represent a tabular dataset as a pie or donut chart; these angles tin then exist passed to an arc generator.
# d3.pie() · Source
Constructs a new pie generator with the default settings.
# pie(data[, arguments…]) · Source
Generates a pie for the given array of data, returning an assortment of objects representing each datum's arc angles. Whatsoever additional arguments are arbitrary; they are merely propagated to the pie generator's accessor functions along with the this object. The length of the returned array is the same as data, and each element i in the returned array corresponds to the element i in the input data. Each object in the returned array has the post-obit properties:
-
data- the input datum; the corresponding chemical element in the input information array. -
value- the numeric value of the arc. -
index- the zero-based sorted index of the arc. -
startAngle- the start angle of the arc. -
endAngle- the end angle of the arc. -
padAngle- the pad angle of the arc.
This representation is designed to piece of work with the arc generator's default startAngle, endAngle and padAngle accessors. The angular units are arbitrary, but if you plan to apply the pie generator in conjunction with an arc generator, you should specify angles in radians, with 0 at -y (12 o'clock) and positive angles proceeding clockwise.
Given a small dataset of numbers, hither is how to compute the arc angles to render this data as a pie chart:
const data = [ ane , 1 , 2 , 3 , 5 , viii , xiii , 21 ] ; const arcs = d3 . pie ( ) ( data ) ; The first pair of parens, pie(), constructs a default pie generator. The second, pie()(data), invokes this generator on the dataset, returning an array of objects:
[ {"information": 1, "value": 1, "index": 6, "startAngle": 6.050474740247008, "endAngle": six.166830023713296, "padAngle": 0}, {"data": 1, "value": 1, "index": seven, "startAngle": half dozen.166830023713296, "endAngle": half dozen.283185307179584, "padAngle": 0}, {"data": ii, "value": 2, "alphabetize": 5, "startAngle": 5.817764173314431, "endAngle": 6.050474740247008, "padAngle": 0}, {"data": 3, "value": 3, "index": 4, "startAngle": v.468698322915565, "endAngle": 5.817764173314431, "padAngle": 0}, {"information": 5, "value": 5, "index": 3, "startAngle": 4.886921905584122, "endAngle": v.468698322915565, "padAngle": 0}, {"data": 8, "value": eight, "index": 2, "startAngle": 3.956079637853813, "endAngle": 4.886921905584122, "padAngle": 0}, {"information": thirteen, "value": 13, "alphabetize": one, "startAngle": 2.443460952792061, "endAngle": 3.956079637853813, "padAngle": 0}, {"data": 21, "value": 21, "index": 0, "startAngle": 0.000000000000000, "endAngle": ii.443460952792061, "padAngle": 0} ] Note that the returned array is in the same order as the data, fifty-fifty though this pie chart is sorted past descending value, starting with the arc for the last datum (value 21) at 12 o'clock.
# pie.value([value]) · Source
If value is specified, sets the value accessor to the specified function or number and returns this pie generator. If value is not specified, returns the current value accessor, which defaults to:
function value ( d ) { return d ; } When a pie is generated, the value accessor volition be invoked for each element in the input data array, being passed the chemical element d, the index i, and the array data equally three arguments. The default value accessor assumes that the input data are numbers, or that they are coercible to numbers using valueOf. If your data are not simply numbers, then you should specify an accessor that returns the corresponding numeric value for a given datum. For instance:
const data = [ { "number": four , "name": "Locke" } , { "number": viii , "proper name": "Reyes" } , { "number": 15 , "proper name": "Ford" } , { "number": xvi , "proper noun": "Jarrah" } , { "number": 23 , "proper noun": "Shephard" } , { "number": 42 , "proper noun": "Kwon" } ] ; const arcs = d3 . pie ( ) . value ( d => d . number ) ( data ) ; This is like to mapping your data to values before invoking the pie generator:
const arcs = d3 . pie ( ) ( data . map ( d => d . number ) ) ; The benefit of an accessor is that the input data remains associated with the returned objects, thereby making it easier to access other fields of the information, for example to set up the color or to add text labels.
# pie.sort([compare]) · Source
If compare is specified, sets the information comparator to the specified function and returns this pie generator. If compare is not specified, returns the current data comparator, which defaults to null. If both the data comparator and the value comparator are zero, then arcs are positioned in the original input gild. Otherwise, the data is sorted according to the data comparator, and the resulting guild is used. Setting the data comparator implicitly sets the value comparator to null.
The compare role takes two arguments a and b, each elements from the input data assortment. If the arc for a should be before the arc for b, then the comparator must render a number less than nada; if the arc for a should exist later the arc for b, then the comparator must return a number greater than zero; returning aught means that the relative lodge of a and b is unspecified. For example, to sort arcs by their associated name:
pie . sort ( ( a , b ) => a . name . localeCompare ( b . proper name ) ) ; Sorting does not bear upon the club of the generated arc array which is always in the same order every bit the input information array; it merely affects the computed angles of each arc. The outset arc starts at the outset bending and the last arc ends at the end angle.
# pie.sortValues([compare]) · Source
If compare is specified, sets the value comparator to the specified role and returns this pie generator. If compare is not specified, returns the current value comparator, which defaults to descending value. The default value comparator is implemented as:
role compare ( a , b ) { return b - a ; } If both the data comparator and the value comparator are null, and then arcs are positioned in the original input society. Otherwise, the data is sorted co-ordinate to the data comparator, and the resulting order is used. Setting the value comparator implicitly sets the data comparator to null.
The value comparator is similar to the information comparator, except the 2 arguments a and b are values derived from the input data array using the value accessor, not the data elements. If the arc for a should be earlier the arc for b, and so the comparator must render a number less than cypher; if the arc for a should be after the arc for b, and then the comparator must return a number greater than cipher; returning zero means that the relative guild of a and b is unspecified. For example, to sort arcs by ascending value:
pie . sortValues ( ( a , b ) => a - b ) ; Sorting does non affect the order of the generated arc array which is ever in the aforementioned guild as the input data array; information technology merely affects the computed angles of each arc. The first arc starts at the start angle and the last arc ends at the finish angle.
# pie.startAngle([angle]) · Source
If angle is specified, sets the overall start angle of the pie to the specified role or number and returns this pie generator. If angle is not specified, returns the current starting time angle accessor, which defaults to:
office startAngle ( ) { render 0 ; } The get-go angle here means the overall showtime bending of the pie, i.eastward., the start angle of the start arc. The outset bending accessor is invoked one time, being passed the same arguments and this context as the pie generator. The units of bending are arbitrary, but if yous plan to apply the pie generator in conjunction with an arc generator, you should specify an angle in radians, with 0 at -y (12 o'clock) and positive angles proceeding clockwise.
# pie.endAngle([angle]) · Source
If angle is specified, sets the overall end angle of the pie to the specified role or number and returns this pie generator. If bending is not specified, returns the current end angle accessor, which defaults to:
function endAngle ( ) { return 2 * Math . PI ; } The terminate bending here means the overall end bending of the pie, i.e., the end angle of the terminal arc. The end angle accessor is invoked once, being passed the aforementioned arguments and this context every bit the pie generator. The units of angle are arbitrary, merely if you lot plan to use the pie generator in conjunction with an arc generator, you should specify an angle in radians, with 0 at -y (12 o'clock) and positive angles proceeding clockwise.
The value of the stop bending is constrained to startAngle ± τ, such that |endAngle - startAngle| ≤ τ.
# pie.padAngle([angle]) · Source
If bending is specified, sets the pad angle to the specified function or number and returns this pie generator. If angle is non specified, returns the current pad bending accessor, which defaults to:
function padAngle ( ) { render 0 ; } The pad angle here means the angular separation between each adjacent arc. The total corporeality of padding reserved is the specified angle times the number of elements in the input information array, and at most |endAngle - startAngle|; the remaining infinite is then divided proportionally by value such that the relative area of each arc is preserved. See the pie padding blitheness for illustration. The pad bending accessor is invoked once, existence passed the same arguments and this context as the pie generator. The units of angle are arbitrary, but if you program to utilise the pie generator in conjunction with an arc generator, you should specify an bending in radians.
Lines
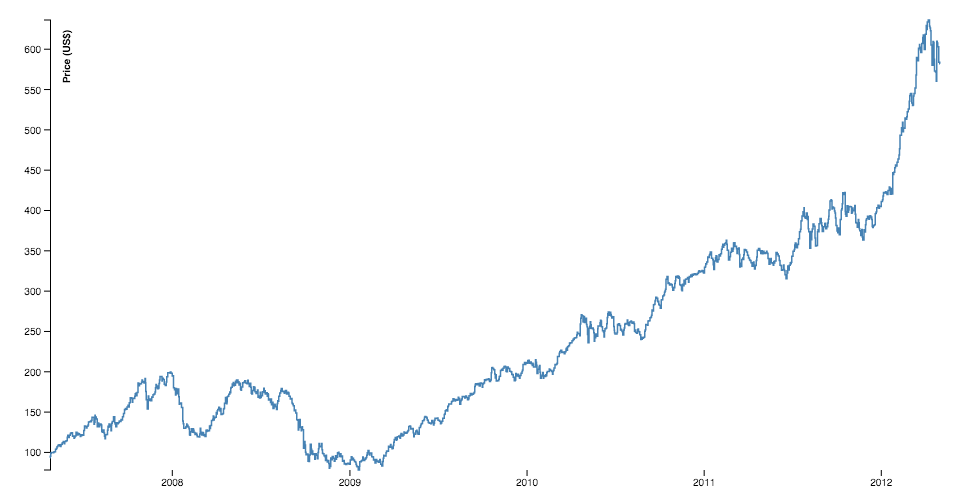
The line generator produces a spline or polyline, as in a line nautical chart. Lines also appear in many other visualization types, such equally the links in hierarchical border bundling.
# d3.line([ten][, y]) · Source, Examples
Constructs a new line generator with the default settings. If x or y are specified, sets the corresponding accessors to the specified function or number and returns this line generator.
# line(information) · Source, Examples
Generates a line for the given array of information. Depending on this line generator's associated bend, the given input data may need to be sorted by 10-value before being passed to the line generator. If the line generator has a context, then the line is rendered to this context as a sequence of path method calls and this role returns void. Otherwise, a path information string is returned.
# line.x([x]) · Source, Examples
If ten is specified, sets the ten accessor to the specified role or number and returns this line generator. If 10 is not specified, returns the current x accessor, which defaults to:
function ten ( d ) { return d [ 0 ] ; } When a line is generated, the ten accessor will be invoked for each defined chemical element in the input data array, being passed the chemical element d, the index i, and the array data as three arguments. The default ten accessor assumes that the input information are two-element arrays of numbers. If your data are in a unlike format, or if you wish to transform the data earlier rendering, then you should specify a custom accessor. For case, if x is a fourth dimension calibration and y is a linear scale:
const information = [ { date: new Date ( 2007 , 3 , 24 ) , value: 93.24 } , { date: new Date ( 2007 , 3 , 25 ) , value: 95.35 } , { engagement: new Date ( 2007 , 3 , 26 ) , value: 98.84 } , { date: new Appointment ( 2007 , 3 , 27 ) , value: 99.92 } , { date: new Date ( 2007 , 3 , 30 ) , value: 99.eighty } , { date: new Date ( 2007 , 4 , 1 ) , value: 99.47 } , … ] ; const line = d3 . line ( ) . x ( d => x ( d . date ) ) . y ( d => y ( d . value ) ) ; # line.y([y]) · Source, Examples
If y is specified, sets the y accessor to the specified part or number and returns this line generator. If y is not specified, returns the current y accessor, which defaults to:
part y ( d ) { return d [ i ] ; } When a line is generated, the y accessor will be invoked for each defined chemical element in the input information array, being passed the chemical element d, the index i, and the assortment data as three arguments. The default y accessor assumes that the input data are two-element arrays of numbers. See line.x for more information.
# line.defined([defined]) · Source, Examples
If defined is specified, sets the defined accessor to the specified function or boolean and returns this line generator. If defined is not specified, returns the current defined accessor, which defaults to:
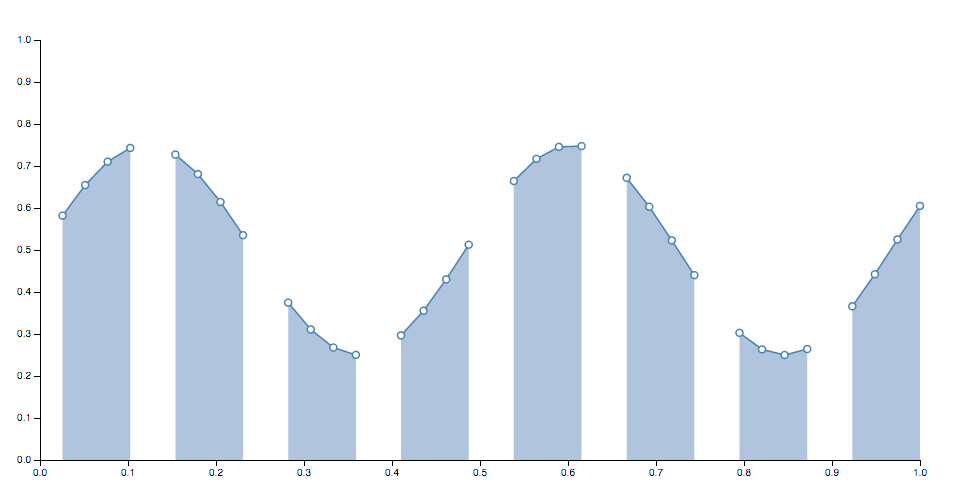
role defined ( ) { return truthful ; } The default accessor thus assumes that the input information is always divers. When a line is generated, the defined accessor will be invoked for each element in the input data array, being passed the chemical element d, the index i, and the assortment data as three arguments. If the given element is defined (i.eastward., if the defined accessor returns a truthy value for this element), the x and y accessors will subsequently be evaluated and the bespeak will be added to the current line segment. Otherwise, the element will be skipped, the current line segment volition be ended, and a new line segment will be generated for the next defined point. As a result, the generated line may take several discrete segments. For example:
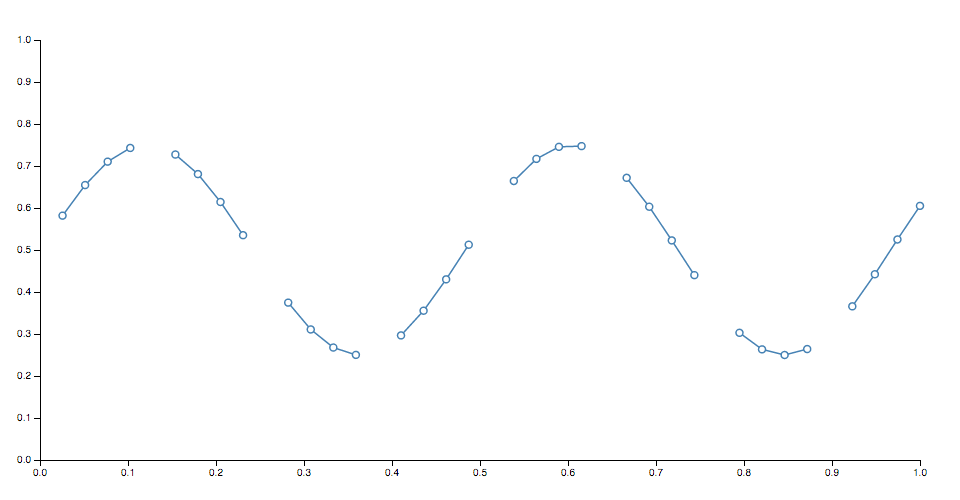
Note that if a line segment consists of but a single betoken, it may appear invisible unless rendered with rounded or square line caps. In addition, some curves such as curveCardinalOpen only render a visible segment if it contains multiple points.
# line.curve([bend]) · Source, Examples
If curve is specified, sets the curve factory and returns this line generator. If curve is not specified, returns the current curve manufacturing plant, which defaults to curveLinear.
# line.context([context]) · Source, Examples
If context is specified, sets the context and returns this line generator. If context is not specified, returns the current context, which defaults to goose egg. If the context is not nix, then the generated line is rendered to this context as a sequence of path method calls. Otherwise, a path data string representing the generated line is returned.
# d3.lineRadial() · Source, Examples

Constructs a new radial line generator with the default settings. A radial line generator is equivalent to the standard Cartesian line generator, except the x and y accessors are replaced with bending and radius accessors. Radial lines are always positioned relative to ⟨0,0⟩; employ a transform (see: SVG, Sail) to change the origin.
# lineRadial(information) · Source, Examples
Equivalent to line.
# lineRadial.angle([angle]) · Source, Examples
Equivalent to line.10, except the accessor returns the angle in radians, with 0 at -y (12 o'clock).
# lineRadial.radius([radius]) · Source, Examples
Equivalent to line.y, except the accessor returns the radius: the altitude from the origin ⟨0,0⟩.
# lineRadial.defined([defined])
Equivalent to line.defined.
# lineRadial.bend([curve]) · Source, Examples
Equivalent to line.bend. Note that curveMonotoneX or curveMonotoneY are not recommended for radial lines because they assume that the data is monotonic in x or y, which is typically untrue of radial lines.
# lineRadial.context([context])
Equivalent to line.context.
Areas
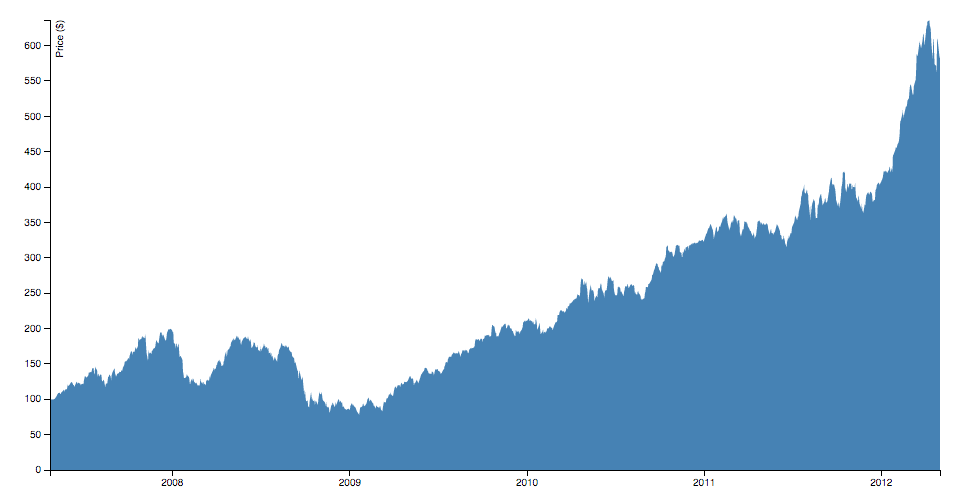
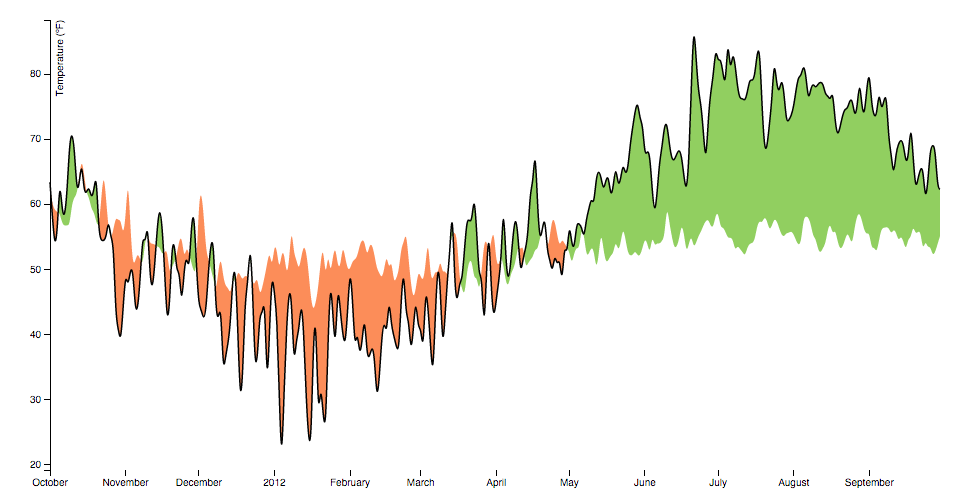
The area generator produces an surface area, as in an area nautical chart. An area is divers by ii bounding lines, either splines or polylines. Typically, the two lines share the aforementioned ten-values (x0 = x1), differing simply in y-value (y0 and y1); most commonly, y0 is defined every bit a constant representing aught. The first line (the topline) is divers by x1 and y1 and is rendered offset; the second line (the baseline) is defined by x0 and y0 and is rendered second, with the points in reverse society. With a curveLinear curve, this produces a clockwise polygon.
# d3.expanse([x][, y0][, y1]) · Source
Constructs a new area generator with the default settings. If x, y0 or y1 are specified, sets the corresponding accessors to the specified role or number and returns this surface area generator.
# expanse(data) · Source
Generates an expanse for the given array of data. Depending on this area generator'southward associated curve, the given input information may need to be sorted by x-value before beingness passed to the area generator. If the expanse generator has a context, then the expanse is rendered to this context equally a sequence of path method calls and this function returns void. Otherwise, a path data string is returned.
# area.ten([x]) · Source
If x is specified, sets x0 to x and x1 to zilch and returns this area generator. If ten is non specified, returns the current x0 accessor.
# area.x0([x]) · Source
If x is specified, sets the x0 accessor to the specified function or number and returns this area generator. If x is not specified, returns the current x0 accessor, which defaults to:
function 10 ( d ) { return d [ 0 ] ; } When an area is generated, the x0 accessor will be invoked for each defined element in the input information array, being passed the chemical element d, the index i, and the array data as three arguments. The default x0 accessor assumes that the input data are two-element arrays of numbers. If your data are in a different format, or if you wish to transform the data before rendering, then you should specify a custom accessor. For example, if x is a time scale and y is a linear scale:
const data = [ { engagement: new Appointment ( 2007 , 3 , 24 ) , value: 93.24 } , { appointment: new Date ( 2007 , 3 , 25 ) , value: 95.35 } , { appointment: new Date ( 2007 , 3 , 26 ) , value: 98.84 } , { date: new Engagement ( 2007 , iii , 27 ) , value: 99.92 } , { date: new Engagement ( 2007 , three , 30 ) , value: 99.80 } , { date: new Appointment ( 2007 , four , i ) , value: 99.47 } , … ] ; const area = d3 . area ( ) . x ( d => x ( d . date ) ) . y1 ( d => y ( d . value ) ) . y0 ( y ( 0 ) ) ; # area.x1([10]) · Source
If x is specified, sets the x1 accessor to the specified function or number and returns this area generator. If x is not specified, returns the current x1 accessor, which defaults to nada, indicating that the previously-computed x0 value should be reused for the x1 value.
When an expanse is generated, the x1 accessor will exist invoked for each divers element in the input data array, being passed the chemical element d, the index i, and the array data as iii arguments. See area.x0 for more information.
# expanse.y([y]) · Source
If y is specified, sets y0 to y and y1 to zip and returns this area generator. If y is non specified, returns the current y0 accessor.
# area.y0([y]) · Source
If y is specified, sets the y0 accessor to the specified function or number and returns this area generator. If y is not specified, returns the current y0 accessor, which defaults to:
function y ( ) { return 0 ; } When an area is generated, the y0 accessor volition be invoked for each defined element in the input information assortment, being passed the element d, the index i, and the array data as three arguments. Meet area.x0 for more than information.
# area.y1([y]) · Source
If y is specified, sets the y1 accessor to the specified role or number and returns this area generator. If y is not specified, returns the current y1 accessor, which defaults to:
function y ( d ) { return d [ ane ] ; } A null accessor is besides allowed, indicating that the previously-computed y0 value should be reused for the y1 value. When an surface area is generated, the y1 accessor will be invoked for each divers element in the input data array, existence passed the element d, the index i, and the assortment information every bit three arguments. See area.x0 for more information.
# area.defined([defined]) · Source
If defined is specified, sets the defined accessor to the specified function or boolean and returns this area generator. If defined is not specified, returns the current defined accessor, which defaults to:
part defined ( ) { render true ; } The default accessor thus assumes that the input data is always defined. When an surface area is generated, the defined accessor will be invoked for each element in the input data assortment, being passed the element d, the alphabetize i, and the array data equally three arguments. If the given chemical element is divers (i.east., if the divers accessor returns a truthy value for this element), the x0, x1, y0 and y1 accessors volition afterward be evaluated and the point volition exist added to the current area segment. Otherwise, the chemical element will be skipped, the current expanse segment volition exist concluded, and a new expanse segment will be generated for the next defined betoken. As a upshot, the generated area may accept several discrete segments. For instance:
Note that if an surface area segment consists of only a single point, it may appear invisible unless rendered with rounded or square line caps. In addition, some curves such as curveCardinalOpen merely return a visible segment if information technology contains multiple points.
# area.curve([curve]) · Source
If curve is specified, sets the bend factory and returns this area generator. If curve is not specified, returns the current bend factory, which defaults to curveLinear.
# area.context([context]) · Source
If context is specified, sets the context and returns this area generator. If context is not specified, returns the current context, which defaults to null. If the context is not nix, then the generated area is rendered to this context as a sequence of path method calls. Otherwise, a path information string representing the generated area is returned.
# surface area.lineX0() · Source
# area.lineY0() · Source
Returns a new line generator that has this surface area generator'due south current defined accessor, curve and context. The line'south 10-accessor is this area'due south x0-accessor, and the line'due south y-accessor is this area'southward y0-accessor.
# area.lineX1() · Source
Returns a new line generator that has this surface area generator'south current divers accessor, curve and context. The line'due south 10-accessor is this expanse's x1-accessor, and the line's y-accessor is this surface area'south y0-accessor.
# area.lineY1() · Source
Returns a new line generator that has this expanse generator'south current defined accessor, bend and context. The line'southward ten-accessor is this area'south x0-accessor, and the line's y-accessor is this surface area's y1-accessor.
# d3.areaRadial() · Source

Constructs a new radial area generator with the default settings. A radial area generator is equivalent to the standard Cartesian expanse generator, except the x and y accessors are replaced with angle and radius accessors. Radial areas are always positioned relative to ⟨0,0⟩; use a transform (see: SVG, Canvas) to change the origin.
# areaRadial(data)
Equivalent to area.
# areaRadial.angle([bending]) · Source
Equivalent to area.x, except the accessor returns the angle in radians, with 0 at -y (12 o'clock).
# areaRadial.startAngle([angle]) · Source
Equivalent to expanse.x0, except the accessor returns the angle in radians, with 0 at -y (12 o'clock). Note: typically angle is used instead of setting separate start and end angles.
# areaRadial.endAngle([angle]) · Source
Equivalent to surface area.x1, except the accessor returns the angle in radians, with 0 at -y (12 o'clock). Notation: typically bending is used instead of setting split up first and end angles.
# areaRadial.radius([radius]) · Source
Equivalent to area.y, except the accessor returns the radius: the altitude from the origin ⟨0,0⟩.
# areaRadial.innerRadius([radius]) · Source
Equivalent to area.y0, except the accessor returns the radius: the distance from the origin ⟨0,0⟩.
# areaRadial.outerRadius([radius]) · Source
Equivalent to expanse.y1, except the accessor returns the radius: the distance from the origin ⟨0,0⟩.
# areaRadial.defined([defined])
Equivalent to surface area.defined.
# areaRadial.curve([curve]) · Source
Equivalent to area.curve. Annotation that curveMonotoneX or curveMonotoneY are not recommended for radial areas because they presume that the data is monotonic in ten or y, which is typically untrue of radial areas.
# areaRadial.context([context])
Equivalent to line.context.
# areaRadial.lineStartAngle() · Source
# areaRadial.lineInnerRadius() · Source
Returns a new radial line generator that has this radial area generator's current defined accessor, curve and context. The line'southward bending accessor is this area'due south offset angle accessor, and the line's radius accessor is this expanse's inner radius accessor.
# areaRadial.lineEndAngle() · Source
Returns a new radial line generator that has this radial surface area generator's current defined accessor, bend and context. The line'due south angle accessor is this area's terminate angle accessor, and the line's radius accessor is this surface area's inner radius accessor.
# areaRadial.lineOuterRadius() · Source
Returns a new radial line generator that has this radial area generator'south electric current defined accessor, curve and context. The line'southward angle accessor is this area's start angle accessor, and the line's radius accessor is this area's outer radius accessor.
Curves
While lines are defined equally a sequence of ii-dimensional [x, y] points, and areas are similarly divers by a topline and a baseline, there remains the task of transforming this discrete representation into a continuous shape: i.east., how to interpolate between the points. A variety of curves are provided for this purpose.
Curves are typically not constructed or used straight, instead being passed to line.curve and expanse.curve. For example:
const line = d3 . line ( d => d . date , d => d . value ) . curve ( d3 . curveCatmullRom . alpha ( 0.five ) ) ; # d3.curveBasis(context) · Source
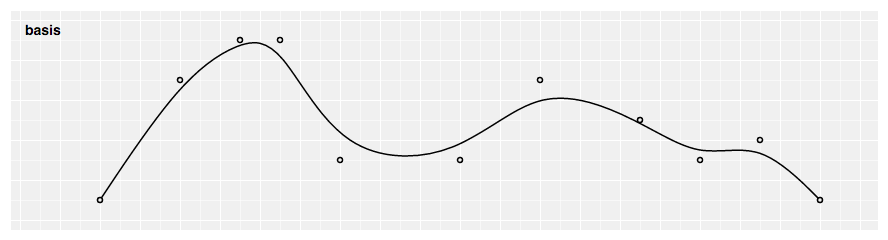
Produces a cubic footing spline using the specified control points. The outset and last points are triplicated such that the spline starts at the first point and ends at the last point, and is tangent to the line between the commencement and 2nd points, and to the line between the penultimate and concluding points.
# d3.curveBasisClosed(context) · Source
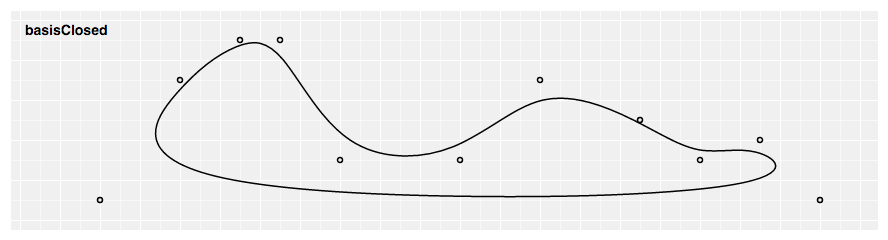
Produces a closed cubic basis spline using the specified control points. When a line segment ends, the first three control points are repeated, producing a closed loop with C2 continuity.
# d3.curveBasisOpen(context) · Source
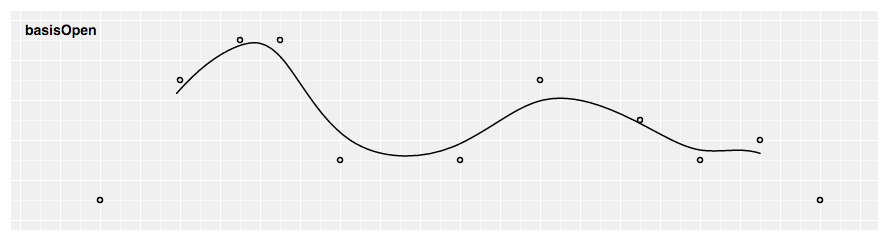
Produces a cubic ground spline using the specified control points. Unlike basis, the first and last points are non repeated, and thus the bend typically does non intersect these points.
# d3.curveBumpX(context) · Source
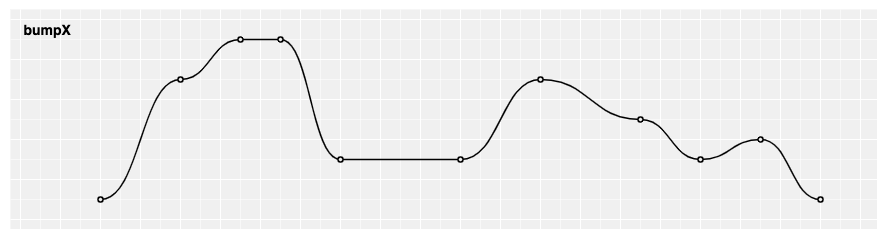
Produces a Bézier curve betwixt each pair of points, with horizontal tangents at each point.
# d3.curveBumpY(context) · Source
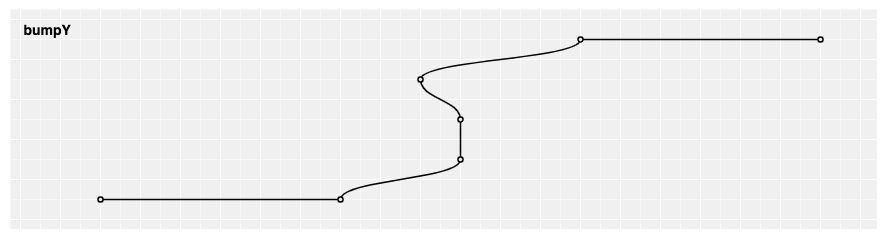
Produces a Bézier curve between each pair of points, with vertical tangents at each point.
# d3.curveBundle(context) · Source
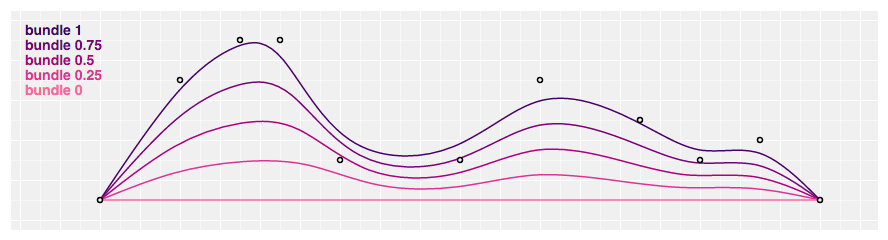
Produces a straightened cubic basis spline using the specified control points, with the spline straightened according to the curve'due south beta, which defaults to 0.85. This curve is typically used in hierarchical edge bundling to disambiguate connections, as proposed by Danny Holten in Hierarchical Edge Bundles: Visualization of Adjacency Relations in Hierarchical Data. This curve does not implement bend.areaStart and curve.areaEnd; it is intended to work with d3.line, not d3.area.
# bundle.beta(beta) · Source
Returns a bundle curve with the specified beta in the range [0, ane], representing the bundle force. If beta equals zero, a directly line betwixt the first and final point is produced; if beta equals i, a standard basis spline is produced. For example:
const line = d3 . line ( ) . curve ( d3 . curveBundle . beta ( 0.5 ) ) ; # d3.curveCardinal(context) · Source

Produces a cubic central spline using the specified control points, with ane-sided differences used for the first and last piece. The default tension is 0.
# d3.curveCardinalClosed(context) · Source

Produces a closed cubic cardinal spline using the specified control points. When a line segment ends, the first three command points are repeated, producing a airtight loop. The default tension is 0.
# d3.curveCardinalOpen(context) · Source
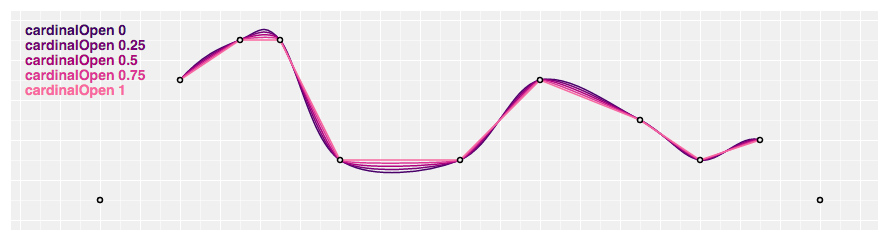
Produces a cubic cardinal spline using the specified control points. Dissimilar curveCardinal, one-sided differences are not used for the first and final piece, and thus the curve starts at the second point and ends at the penultimate point. The default tension is 0.
# key.tension(tension) · Source
Returns a cardinal curve with the specified tension in the range [0, 1]. The tension determines the length of the tangents: a tension of 1 yields all zero tangents, equivalent to curveLinear; a tension of zero produces a uniform Catmull–Rom spline. For case:
const line = d3 . line ( ) . bend ( d3 . curveCardinal . tension ( 0.v ) ) ; # d3.curveCatmullRom(context) · Source
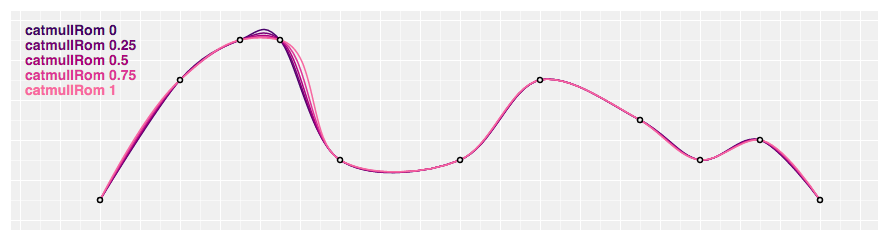
Produces a cubic Catmull–Rom spline using the specified command points and the parameter blastoff, which defaults to 0.5, as proposed past Yuksel et al. in On the Parameterization of Catmull–Rom Curves, with ane-sided differences used for the beginning and terminal piece.
# d3.curveCatmullRomClosed(context) · Source
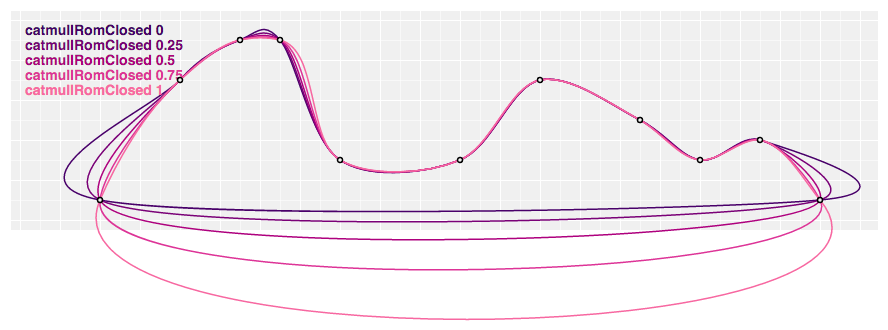
Produces a closed cubic Catmull–Rom spline using the specified command points and the parameter alpha, which defaults to 0.v, as proposed past Yuksel et al. When a line segment ends, the beginning three command points are repeated, producing a closed loop.
# d3.curveCatmullRomOpen(context) · Source
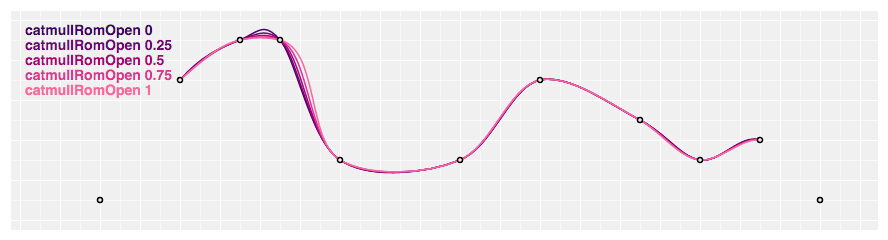
Produces a cubic Catmull–Rom spline using the specified control points and the parameter alpha, which defaults to 0.5, as proposed past Yuksel et al. Dissimilar curveCatmullRom, one-sided differences are not used for the first and last piece, and thus the curve starts at the second point and ends at the penultimate signal.
# catmullRom.alpha(blastoff) · Source
Returns a cubic Catmull–Rom curve with the specified alpha in the range [0, ane]. If alpha is nil, produces a compatible spline, equivalent to curveCardinal with a tension of zero; if alpha is one, produces a chordal spline; if blastoff is 0.v, produces a centripetal spline. Centripetal splines are recommended to avert cocky-intersections and overshoot. For instance:
const line = d3 . line ( ) . bend ( d3 . curveCatmullRom . alpha ( 0.5 ) ) ; # d3.curveLinear(context) · Source
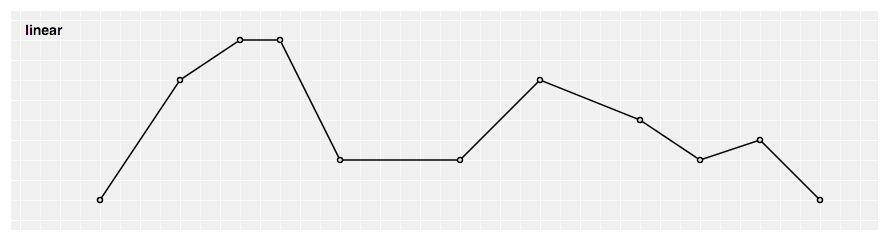
Produces a polyline through the specified points.
# d3.curveLinearClosed(context) · Source
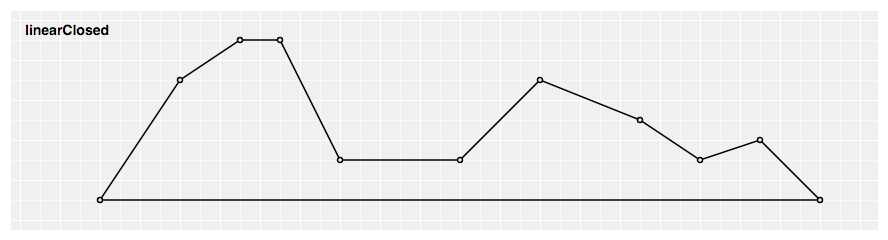
Produces a closed polyline through the specified points by repeating the kickoff betoken when the line segment ends.
# d3.curveMonotoneX(context) · Source
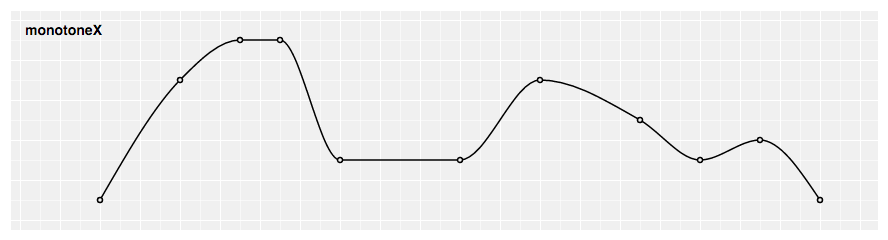
Produces a cubic spline that preserves monotonicity in y, assuming monotonicity in 10, as proposed by Steffen in A uncomplicated method for monotonic interpolation in ane dimension: "a smooth bend with continuous first-order derivatives that passes through any given ready of data points without spurious oscillations. Local extrema can occur only at grid points where they are given by the information, merely not in between two adjacent grid points."
# d3.curveMonotoneY(context) · Source
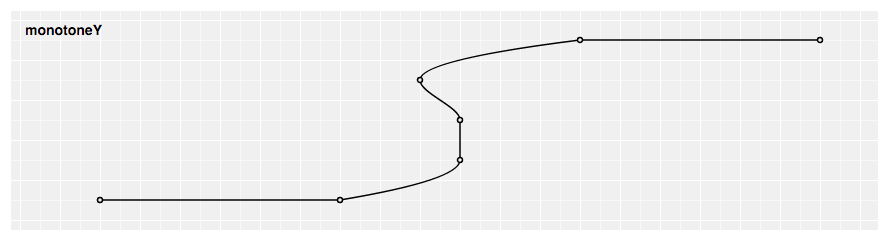
Produces a cubic spline that preserves monotonicity in x, assuming monotonicity in y, every bit proposed past Steffen in A uncomplicated method for monotonic interpolation in one dimension: "a shine curve with continuous start-order derivatives that passes through whatsoever given set of information points without spurious oscillations. Local extrema tin can occur but at grid points where they are given past the data, but not in betwixt 2 adjacent grid points."
# d3.curveNatural(context) · Source
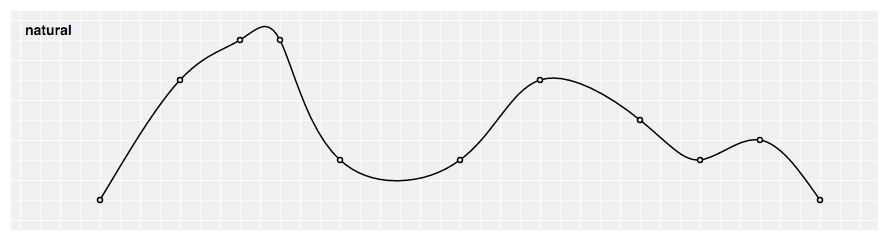
Produces a natural cubic spline with the 2nd derivative of the spline set to zilch at the endpoints.
# d3.curveStep(context) · Source
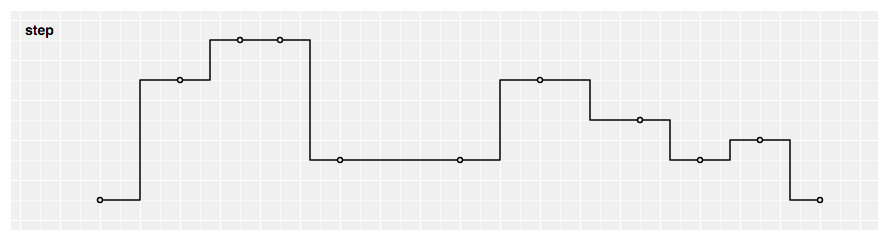
Produces a piecewise abiding office (a step function) consisting of alternating horizontal and vertical lines. The y-value changes at the midpoint of each pair of adjacent x-values.
# d3.curveStepAfter(context) · Source
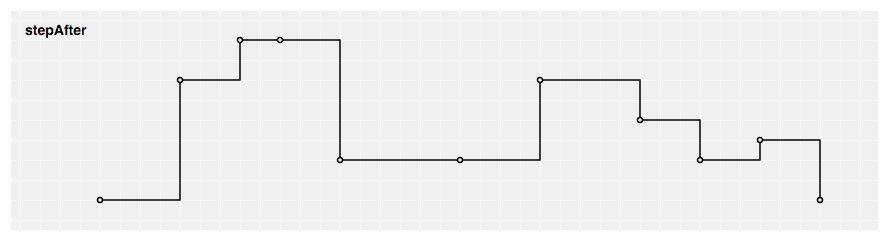
Produces a piecewise constant office (a pace function) consisting of alternating horizontal and vertical lines. The y-value changes afterwards the 10-value.
# d3.curveStepBefore(context) · Source
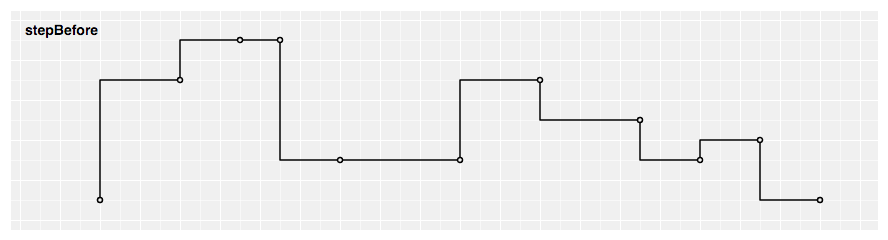
Produces a piecewise constant role (a step office) consisting of alternating horizontal and vertical lines. The y-value changes before the x-value.
Custom Curves
Curves are typically non used directly, instead being passed to line.curve and expanse.bend. Nonetheless, you tin can define your own bend implementation should none of the built-in curves satisfy your needs using the post-obit interface. Yous tin as well use this low-level interface with a born curve type as an alternative to the line and expanse generators.
# curve.areaStart() · Source
Indicates the start of a new area segment. Each area segment consists of exactly two line segments: the topline, followed by the baseline, with the baseline points in reverse social club.
# curve.areaEnd() · Source
Indicates the terminate of the electric current area segment.
# curve.lineStart() · Source
Indicates the first of a new line segment. Zero or more points will follow.
# curve.lineEnd() · Source
Indicates the stop of the current line segment.
# bend.point(x, y) · Source
Indicates a new point in the current line segment with the given ten- and y-values.
Links
The link shape generates a polish cubic Bézier bend from a source point to a target point. The tangents of the curve at the start and end are either vertical, horizontal or radial.
# d3.link(bend) · Source
Returns a new link generator using the specified curve. For case, to visualize links in a tree diagram rooted on the top border of the display, yous might say:
const link = d3 . link ( d3 . curveBumpY ) . x ( d => d . x ) . y ( d => d . y ) ; # d3.linkVertical() · Source
Shorthand for d3.link with d3.curveBumpY; suitable for visualizing links in a tree diagram rooted on the top edge of the display. Equivalent to:
const link = d3 . link ( d3 . curveBumpY ) ; # d3.linkHorizontal() · Source
Shorthand for d3.link with d3.curveBumpX; suitable for visualizing links in a tree diagram rooted on the left edge of the display. Equivalent to:
const link = d3 . link ( d3 . curveBumpX ) ; # link(arguments…) · Source
Generates a link for the given arguments. The arguments are arbitrary; they are simply propagated to the link generator's accessor functions along with the this object. For example, with the default settings, an object expected:
link ( { source: [ 100 , 100 ] , target: [ 300 , 300 ] } ) ; # link.source([source]) · Source
If source is specified, sets the source accessor to the specified function and returns this link generator. If source is not specified, returns the electric current source accessor, which defaults to:
function source ( d ) { return d . source ; } # link.target([target]) · Source
If target is specified, sets the target accessor to the specified function and returns this link generator. If target is not specified, returns the current target accessor, which defaults to:
function target ( d ) { return d . target ; } # link.x([10]) · Source
If x is specified, sets the x-accessor to the specified function or number and returns this link generator. If x is not specified, returns the current x-accessor, which defaults to:
office x ( d ) { return d [ 0 ] ; } # link.y([y]) · Source
If y is specified, sets the y-accessor to the specified function or number and returns this link generator. If y is not specified, returns the current y-accessor, which defaults to:
role y ( d ) { return d [ i ] ; } # link.context([context]) · Source
If context is specified, sets the context and returns this link generator. If context is not specified, returns the current context, which defaults to null. If the context is not null, then the generated link is rendered to this context as a sequence of path method calls. Otherwise, a path data cord representing the generated link is returned. See likewise d3-path.
# d3.linkRadial() · Source
Returns a new link generator with radial tangents. For example, to visualize links in a tree diagram rooted in the center of the brandish, you might say:
const link = d3 . linkRadial ( ) . angle ( d => d . x ) . radius ( d => d . y ) ; # linkRadial.angle([angle]) · Source
Equivalent to link.x, except the accessor returns the angle in radians, with 0 at -y (12 o'clock).
# linkRadial.radius([radius]) · Source
Equivalent to link.y, except the accessor returns the radius: the distance from the origin ⟨0,0⟩.
Symbols
Symbols provide a chiselled shape encoding equally is commonly used in scatterplots. Symbols are always centered at ⟨0,0⟩; employ a transform (see: SVG, Canvas) to move the symbol to a different position.
# d3.symbol([type][, size]) · Source, Examples
Constructs a new symbol generator of the specified blazon and size. If non specified, type defaults to a circle, and size defaults to 64.
# symbol(arguments…) · Source
Generates a symbol for the given arguments. The arguments are arbitrary; they are only propagated to the symbol generator's accessor functions forth with the this object. For example, with the default settings, no arguments are needed to produce a circumvolve with area 64 square pixels. If the symbol generator has a context, then the symbol is rendered to this context as a sequence of path method calls and this office returns void. Otherwise, a path information string is returned.
# symbol.type([type]) · Source
If type is specified, sets the symbol blazon to the specified office or symbol type and returns this symbol generator. If type is a role, the symbol generator'southward arguments and this are passed through. (Meet choice.attr if yous are using d3-selection.) If type is non specified, returns the electric current symbol type accessor, which defaults to:
function type ( ) { return circle ; } See symbolsFill and symbolsStroke for congenital-in symbol types. To implement a custom symbol blazon, pass an object that implements symbolType.depict.
# symbol.size([size]) · Source
If size is specified, sets the size to the specified function or number and returns this symbol generator. If size is a function, the symbol generator'southward arguments and this are passed through. (Come across option.attr if you are using d3-selection.) If size is not specified, returns the current size accessor, which defaults to:
function size ( ) { return 64 ; } Specifying the size as a office is useful for amalgam a scatterplot with a size encoding. If you lot wish to scale the symbol to fit a given bounding box, rather than by area, try SVG'southward getBBox.
# symbol.context([context]) · Source
If context is specified, sets the context and returns this symbol generator. If context is not specified, returns the current context, which defaults to null. If the context is not zip, and so the generated symbol is rendered to this context as a sequence of path method calls. Otherwise, a path data string representing the generated symbol is returned.
# d3.symbolsFill · Source






An assortment containing a set of symbol types designed for filling: circle, cantankerous, diamond, square, star, triangle, and wye. Useful for constructing the range of an ordinal scale should you wish to use a shape encoding for categorical data.
# d3.symbolsStroke · Source
An array containing a prepare of symbol types designed for stroking: circle, plus, ten, triangle2, asterisk, square2, and diamond2. Useful for constructing the range of an ordinal scale should yous wish to use a shape encoding for categorical information.
# d3.symbolAsterisk · Source
The asterisk symbol type; intended for stroking.
# d3.symbolCircle · Source
The circumvolve symbol type; intended for either filling or stroking.
# d3.symbolCross · Source
The Greek cross symbol type, with arms of equal length; intended for filling.
# d3.symbolDiamond · Source
The rhombus symbol blazon; intended for filling.
# d3.symbolDiamond2 · Source
The rotated foursquare symbol type; intended for stroking.
# d3.symbolPlus · Source
The plus symbol type; intended for stroking.
# d3.symbolSquare · Source
The square symbol type; intended for filling.
# d3.symbolSquare2 · Source
The square2 symbol type; intended for stroking.
# d3.symbolStar · Source
The pentagonal star (pentagram) symbol type; intended for filling.
# d3.symbolTriangle · Source
The upward-pointing triangle symbol type; intended for filling.
# d3.symbolTriangle2 · Source
The up-pointing triangle symbol type; intended for stroking.
# d3.symbolWye · Source
The Y-shape symbol type; intended for filling.
# d3.symbolX · Source
The X-shape symbol type; intended for stroking.
# d3.pointRadial(angle, radius) · Source, Examples
Returns the point [x, y] for the given angle in radians, with 0 at -y (12 o'clock) and positive angles proceeding clockwise, and the given radius.
Custom Symbol Types
Symbol types are typically not used directly, instead existence passed to symbol.blazon. However, you can define your own symbol type implementation should none of the built-in types satisfy your needs using the following interface. You can too use this low-level interface with a congenital-in symbol blazon equally an culling to the symbol generator.
# symbolType.draw(context, size)
Renders this symbol type to the specified context with the specified size in square pixels. The context implements the CanvasPathMethods interface. (Note that this is a subset of the CanvasRenderingContext2D interface!)
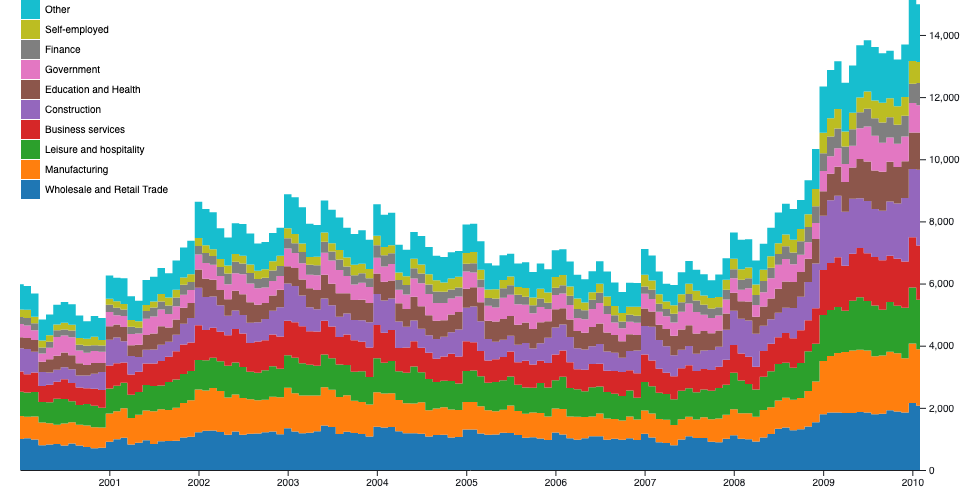
Stacks
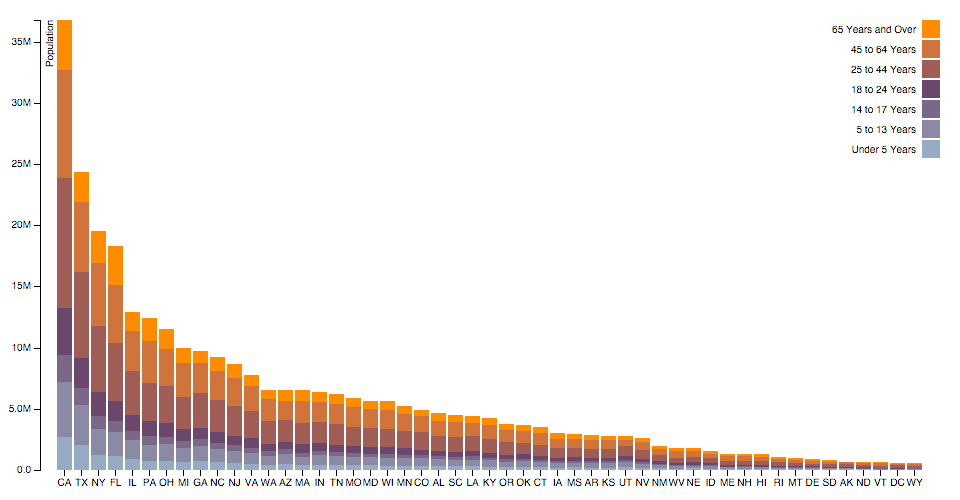
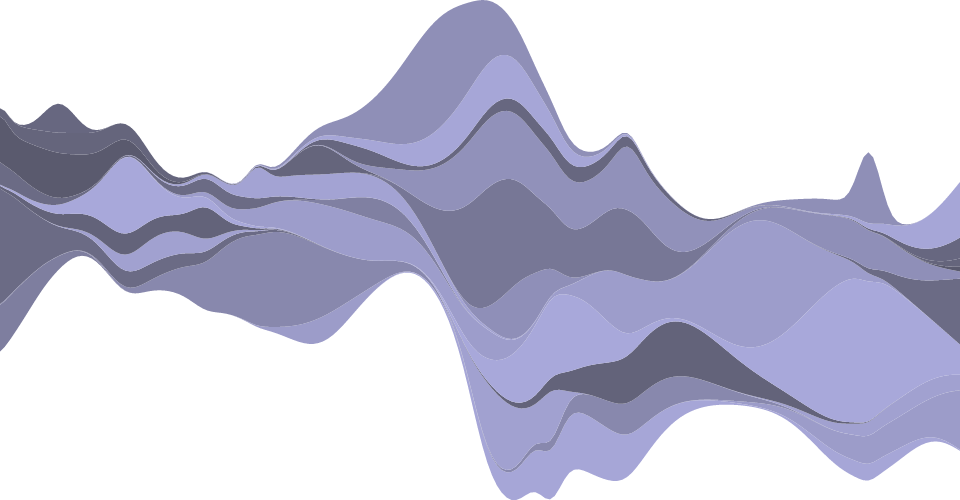
Some shape types tin be stacked, placing one shape next to another. For example, a bar chart of monthly sales might be broken down into a multi-series bar chart by product category, stacking bars vertically. This is equivalent to subdividing a bar chart past an ordinal dimension (such as product category) and applying a color encoding.
Stacked charts can show overall value and per-category value simultaneously; however, it is typically harder to compare across categories, as only the bottom layer of the stack is aligned. So, chose the stack order carefully, and consider a streamgraph. (See also grouped charts.)
Like the pie generator, the stack generator does not produce a shape directly. Instead it computes positions which you can and then pass to an expanse generator or use direct, say to position bars.
# d3.stack() · Source
Constructs a new stack generator with the default settings.
# stack(data[, arguments…]) · Source
Generates a stack for the given array of information, returning an array representing each series. Whatever additional arguments are arbitrary; they are but propagated to accessors along with the this object.
The series are determined past the keys accessor; each series i in the returned assortment corresponds to the ith key. Each serial is an array of points, where each point j corresponds to the jth element in the input data. Lastly, each point is represented as an array [y0, y1] where y0 is the lower value (baseline) and y1 is the upper value (topline); the difference between y0 and y1 corresponds to the computed value for this point. The key for each serial is available every bit serial.key, and the index as series.alphabetize. The input information element for each bespeak is available as point.data.
For case, consider the following table representing monthly sales of fruits:
| Month | Apples | Bananas | Cherries | Dates |
|---|---|---|---|---|
| ane/2015 | 3840 | 1920 | 960 | 400 |
| 2/2015 | 1600 | 1440 | 960 | 400 |
| 3/2015 | 640 | 960 | 640 | 400 |
| 4/2015 | 320 | 480 | 640 | 400 |
This might be represented in JavaScript as an array of objects:
const data = [ { month: new Date ( 2015 , 0 , 1 ) , apples: 3840 , bananas: 1920 , cherries: 960 , dates: 400 } , { month: new Date ( 2015 , ane , 1 ) , apples: 1600 , bananas: 1440 , cherries: 960 , dates: 400 } , { month: new Appointment ( 2015 , 2 , one ) , apples: 640 , bananas: 960 , cherries: 640 , dates: 400 } , { month: new Date ( 2015 , 3 , 1 ) , apples: 320 , bananas: 480 , cherries: 640 , dates: 400 } ] ; To produce a stack for this information:
const stack = d3 . stack ( ) . keys ( [ "apples" , "bananas" , "cherries" , "dates" ] ) . order ( d3 . stackOrderNone ) . first ( d3 . stackOffsetNone ) ; const series = stack ( data ) ; The resulting array has one element per series. Each serial has one point per month, and each point has a lower and upper value defining the baseline and topline:
[ [ [ 0 , 3840 ] , [ 0 , 1600 ] , [ 0 , 640 ] , [ 0 , 320 ] ] , // apples [ [ 3840 , 5760 ] , [ 1600 , 3040 ] , [ 640 , 1600 ] , [ 320 , 800 ] ] , // bananas [ [ 5760 , 6720 ] , [ 3040 , 4000 ] , [ 1600 , 2240 ] , [ 800 , 1440 ] ] , // cherries [ [ 6720 , 7120 ] , [ 4000 , 4400 ] , [ 2240 , 2640 ] , [ 1440 , 1840 ] ] , // dates ] Each series in then typically passed to an area generator to render an area chart, or used to construct rectangles for a bar chart.
# stack.keys([keys]) · Source
If keys is specified, sets the keys accessor to the specified office or array and returns this stack generator. If keys is non specified, returns the current keys accessor, which defaults to the empty array. A serial (layer) is generated for each key. Keys are typically strings, just they may be arbitrary values. The series' key is passed to the value accessor, along with each data indicate, to compute the point's value.
# stack.value([value]) · Source
If value is specified, sets the value accessor to the specified function or number and returns this stack generator. If value is not specified, returns the current value accessor, which defaults to:
function value ( d , key ) { return d [ central ] ; } Thus, past default the stack generator assumes that the input information is an array of objects, with each object exposing named properties with numeric values; see stack for an example.
# stack.order([guild]) · Source
If social club is specified, sets the order accessor to the specified function or array and returns this stack generator. If order is not specified, returns the current order accessor, which defaults to stackOrderNone; this uses the club given past the primal accessor. See stack orders for the born orders.
If order is a function, it is passed the generated series array and must return an array of numeric indexes representing the stack club. For example, the default order is defined every bit:
function orderNone ( series ) { allow n = series . length ; const o = new Array ( due north ) ; while ( -- n >= 0 ) o [ n ] = n ; return o ; } The stack gild is computed prior to the offset; thus, the lower value for all points is zero at the time the order is computed. The index attribute for each series is too non fix until after the club is computed.
# stack.outset([offset]) · Source
If first is specified, sets the offset accessor to the specified function and returns this stack generator. If offset is non specified, returns the electric current offset acccesor, which defaults to stackOffsetNone; this uses a nix baseline. See stack offsets for the born offsets.
The commencement part is passed the generated series array and the gild index array; it is then responsible for updating the lower and upper values in the series assortment. For example, the default offset is divers as:
function offsetNone ( series , society ) { if ( ! ( ( north = series . length ) > i ) ) render ; for ( permit i = ane , s0 , s1 = series [ order [ 0 ] ] , northward , m = s1 . length ; i < n ; ++ i ) { s0 = s1 , s1 = series [ club [ i ] ] ; for ( let j = 0 ; j < m ; ++ j ) { s1 [ j ] [ i ] += s1 [ j ] [ 0 ] = s0 [ j ] [ 1 ] ; } } } Stack Orders
Stack orders are typically non used directly, but are instead passed to stack.society.
# d3.stackOrderAppearance(series) · Source
Returns a series order such that the earliest serial (according to the maximum value) is at the lesser.
# d3.stackOrderAscending(serial) · Source
Returns a serial guild such that the smallest series (according to the sum of values) is at the bottom.
# d3.stackOrderDescending(series) · Source
Returns a series order such that the largest series (co-ordinate to the sum of values) is at the bottom.
# d3.stackOrderInsideOut(series) · Source
Returns a series lodge such that the earliest series (according to the maximum value) are on the inside and the afterward serial are on the outside. This order is recommended for streamgraphs in conjunction with the jerk showtime. See Stacked Graphs—Geometry & Aesthetics past Byron & Wattenberg for more information.
# d3.stackOrderNone(serial) · Source
Returns the given series social club [0, 1, … northward - 1] where north is the number of elements in series. Thus, the stack order is given by the fundamental accessor.
# d3.stackOrderReverse(series) · Source
Returns the reverse of the given series society [due north - i, due north - 2, … 0] where n is the number of elements in series. Thus, the stack order is given past the opposite of the key accessor.
Stack Offsets
Stack offsets are typically non used directly, but are instead passed to stack.starting time.
# d3.stackOffsetExpand(series, social club) · Source
Applies a zilch baseline and normalizes the values for each point such that the topline is always i.
# d3.stackOffsetDiverging(serial, club) · Source
Positive values are stacked above nil, negative values are stacked beneath zero, and zero values are stacked at zero.
# d3.stackOffsetNone(serial, guild) · Source
Applies a nix baseline.
# d3.stackOffsetSilhouette(series, society) · Source
Shifts the baseline downwards such that the center of the streamgraph is always at zero.
# d3.stackOffsetWiggle(serial, order) · Source
Shifts the baseline so as to minimize the weighted jerk of layers. This showtime is recommended for streamgraphs in conjunction with the inside-out order. See Stacked Graphs—Geometry & Aesthetics by Bryon & Wattenberg for more information.
Source: https://github.com/d3/d3-shape
0 Response to "weird 3d shapes to draw"
Post a Comment